In this blog post, I will solve the second part of problem 3 from the Indian National Mathematical Olympiad (INMO) 2016. I hope you enjoy my solution!!

In this blog post, I will solve the first part of problem 3 from the Indian National Mathematical Olympiad (INMO) 2016. I personally found this problem really interesting and it forced me to think innovatively. I hope you enjoy reading my solution!! The solution to part 2 will be released shortly.

In this blog post, I will solve problem 3 from the Indian National Mathematical Olympiad (INMO) 2019. I personally found this problem very interesting and fun to solve. I hope you enjoy reading my solution!!

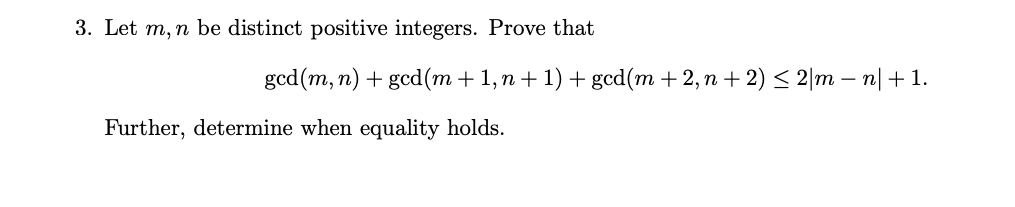
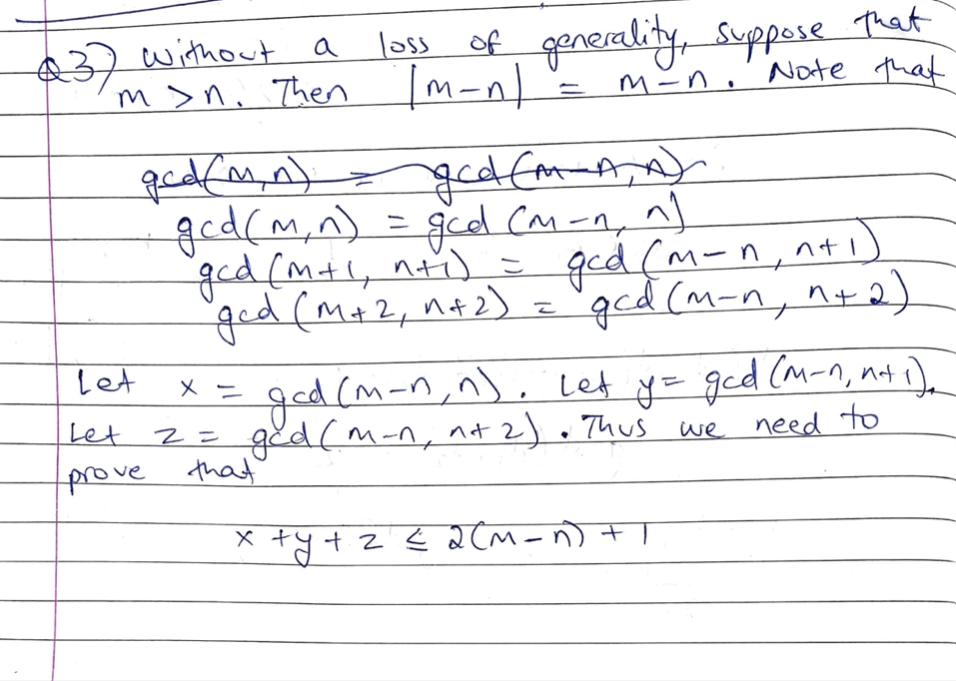
In this blog post, I will solve problem 2 from the 31st Indian National Mathematical Olympiad – 2016, which in my opinion lends deep insight into solving problems involving inequalities. I hope you enjoy reading my solution!!

Problem:

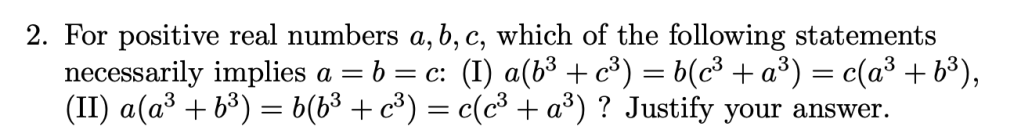
Solution:

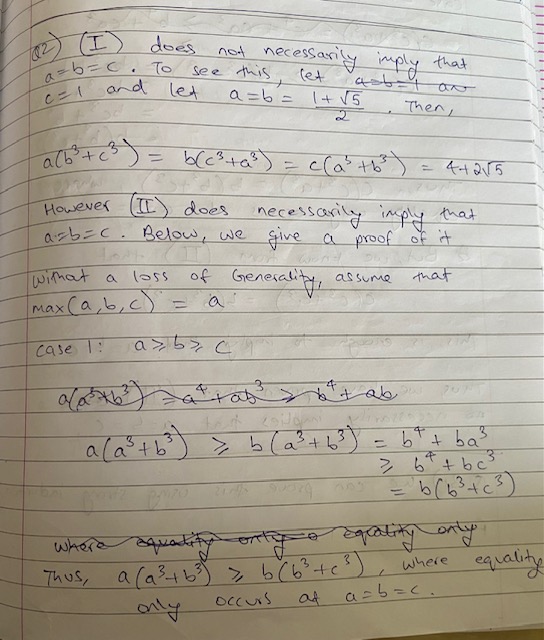
In today’s blog post, I want to give an answer to the following question: what is the precise mathematical definition of a limit?

For instance, what do I actually mean when I say that the limit of f(x) as x approaches a is L? Well, the first thought that may have come to your mind is that f(x) “approaches” L as x “approaches” a. But, what is the meaning of “approach”?. for example, if I let f(x) = x² and I say that x gets closer and closer to 0, then one may also argue that f(x) is “approaching” -1, as while f(x) gets closer and closer to 0, it also gets closer and closer to -1. However, we know that this is not the case.

So, how do we answer this question? Well, one way of thinking about this is that f(x) should get “arbitrarily close” to L, i.e. that no matter how small a number n I choose, be it 1/100, 1/1000 or even 1/10¹⁰⁰, there exists a sufficiently small interval around a such that if x gets close enough to a so as to belong in that interval, then the difference between f(x) and L is smaller than n. With this idea, we have stumbled upon the true meaning of a limit in mathematics, and below, I give the formal definition of a limit as is used in real analysis which is based on the idea developed in the previous sentence.

Let f(x) be a function defined on an open interval around x = a (note that f(a) need not be defined). We say that the limit as x approaches a is L if for every ε > 0, there exists δ > 0 such that for all values of x, 0 < |x – a| < δ implies that |f(x) – L| < ε.

I hope you enjoyed pondering the question which I addressed in this blog post!!

This is a complicated-looking number theory problem which can be solved by a few clever observations. I hope you enjoy reading through my solution!!

This is a very interesting limit problem which gives a tonne of insight into the spellbinding idea of limits. I hope you enjoy reading through my solution!!

This is an integration problem with a very fascinating solution, and I feel that it is a must read for all math enthusiasts (I have given a hint at the solution in the problem title).

Thanks to Liam for giving me this problem

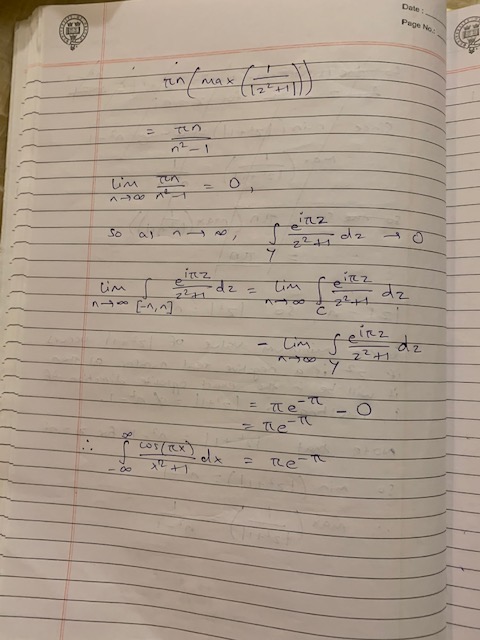
Problem: Find all positive integers n such that n + 1 is a factor of n² + 1.

Solution: Firstly, note that (n + 1)² = n² + 2n + 1 is always divisible by n + 1. So, if n² + 1 is divisible by n + 1, then (n + 1)² – (n² + 1) = 2n must also be divisible by n + 1. Furthermore, it is easy to see that 2(n + 1) = 2n + 2 is also divisible by n + 1. Since both 2n and 2n + 2 must be divisible by n + 1, 2n + 2 – 2n = 2 must also be divisible by n + 1. Hence n + 1 can only be equal to 1 or 2, as these are the only divisors of 2. Therefore n can only be equal to 1 or 0. Recall that n is a positive integer, so the only possible value of n is 1. Therefore, if n + 1 divides n² + 1, the only possible value of n is 1. Now all that is left is to check that 1 is actually a valid solution, as we cannot just come to that conclusion by only knowing that 1 is a possible solution. 1 + 1 = 2 is a factor of 1² + 1 = 2, hence 1 is indeed a valid solution.

Hence, we have shown that n = 1 is the only solution to this problem. This is a simple example of an argument in elementary number theory, and I hope you enjoyed working through it!!

Don’t forget to check my blog soon for another fascinating problem!!

Problem: Suppose that you are in an airplane that has been hijacked by a group of terrorists, and that exactly 1% of the people on the airplane are terrorists. Luckily, there is a police officer on the plane who is 99% accurate at detecting terrorists: If you are a terrorist, then he will classify you as a terrorist 99% of the time, and if you are not a terrorist, then he will classify you as innocent 99% of the time. He classifies the first person as a terrorist. What is the probability that the first person is actually a terrorist

Solution: Now, at first you may feel that the odds of the first person being a terrorist is extremely high. After all, the police officer has a 99% accuracy. However, this is not the case at all, as we shall see below that the probability of the first person actually being a terrorist is just 50% !

Now, let’s first consider the probability of the first person being innocent and him being classified as a terrorist. The probability of the first person being innocent is 99%. However, the probability that the first person is classified as a terrorist given that he is innocent is just 1%, as the police officer has 99% accuracy. So the probability of him being innocent and classified as a terrorist is 0.99 * 0.01 = 0.0099 = 0.99%.

Now, let’s consider the probability of the first person being a terrorist and him being classified as a terrorist. The probability of the person being a terrorist is 1%. The probability that he is classified as a terrorist given that he is a terrorist is 99%, owing to the police officer’s 99% accuracy. So the probability of him being a terrorist and him being classified as a terrorist is 0.01 * 0.99 = 0.0099 = 0.99%.

So both of these cases have the same probability! When we say that the police officer classifies the first person as a terrorist, the universal set of all possible outcomes is restricted to the two cases considered above, and since both of these cases are equally likely, both of them must have the same probability. Since the probabilities must add up to 100% and both of the probabilities are equal, both of the probabilities must be 50% !!

So the probability that the person was actually a terrorist is just 50%, as stated earlier. This at first seems like a pretty counterintuitive result as despite the police officer’s superhuman accuracy, there is just a 50% chance that the person is actually a terrorist. However, as our argument illustrates, this is the truth. This problem comes from an extremely interesting topic in mathematics called as conditional probability, which I would urge you to explore further if you are a fellow math enthusiast.

Don’t forget to check my blog next week for another fascinating problem!!