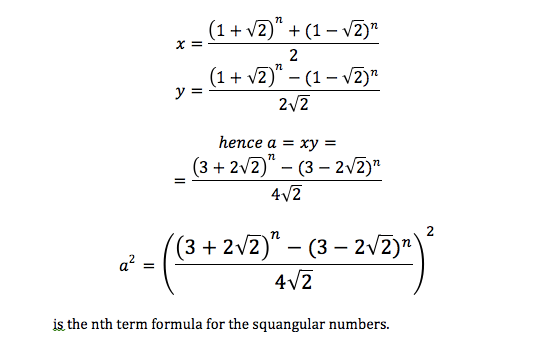Problem: Find out whether 1634829⁸³⁶⁵² + 6738213⁹²⁶³⁴ is divisible by 4.

Solution: Now, at first this problem seems out of reach for any human mind in the world due to the sheer immensity of this number, but trust me, its actually not that difficult once you make some observations.

First, let me clarify a bit of terminology. note that if two integers a and b are said to be congruent to each other modulo p, it means that a and b leave the same remainder when divided by p. For example, 8 is congruent to 3 modulo 5 because both 8 and 3 leave a remainder of 3 when divided by 5.

Result 1: The sum of two numbers is congruent to the sum of their remainders when divided by p modulo p. Proof: Let the two numbers be a and b, and let their remainders be c and d respectively. Let c + d = kp + r (It leaves a remainder of r modulo p). a + b = (ep + c) + (fp + d) = (e + f + k)p + r. So a + b also leaves a remainder of r modulo p, as desired.

Result 2: The product of two numbers is congruent to the product of their remainders when divided by p modulo p. Proof: Let the two numbers be a and b, and let their remainders be c and d respectively. Let cd = kp + r (It leaves a remainder of r modulo p). ab = (ep + c)(fp + d) = (efp + ed + cf + k)p + r. So ab also leaves a remainder of r modulo p, as desired.

Now note that both the exponents in the question are even whereas both bases are odd. An odd number either leaves a remainder of 1 or 3 modulo 4. However, an odd square is congruent to 1*1 = 1 or 3*3 = 9 = 1 modulo 4 (Using Result 2). So an odd square always leaves a remainder of 1 modulo 4. Both terms in the question are an odd number raised to the power of an even number, which can be re-written as an odd square raised to an integer power (as an even number is 2 * an integer).

So, using result 2, the first term is congruent to 1 ^ (83652/2) and the second term is congruent to 1 ^ (92634/2), which are both equal to 1 (Recall that 83652 and 92634 were the exponents in the question). Using result 1, I know that their sum leaves a remainder of 1 + 1 = 2, so the expression in the problem leaves a remainder of 2 when divided by 4. Hence, the answer is that 1634829⁸³⁶⁵² + 6738213⁹²⁶³⁴ is not divisible by 4!!

More generally, any number of the form odd^even + odd^even is not divisible by 4. This can easily be seen from the solution, as the only property of the numbers in the question which was utilised by us was whether they are odd or even.

Don’t forget to check my blog next week for another fascinating problem!!

Problem: I am currently standing on the number line at the number 0, and I am allowed to make two types of moves. Firstly, I can move 17 to the right or left. Secondly, I can move 41 to the right or left. So, which positive integers on the number line can be reached using these two moves.

Solution: All positive integers can be reached using these two moves. To see this, first notice that we can reach the positive integer n given that n is a linear combination of 17 and 41, meaning that n = 17a + 41b for some integers a and b. Now, consider the tuple of positive integers (17, 41). It is trivial to see that both 17 and 41 can be reached to using the moves specified in the problem. Now we create a sequence of such tuples with the rule being that if the current term is (a, b), with a >= b, then the next term will be (a – b, b). (Note that the tuples considered are unordered, i.e. The order of the elements in the tuple does not matter)

Note that each positive integer in every tuple of this sequence can be reached using the two moves given in the problem statement! This can simply be proven using induction. As mentioned earlier, it is obvious that 17 and 41 can be reached, so the basis case is trivial. Now if I know that I can reach a and b using these moves, then a and b are linear combinations of the integers 17 and 41, so their difference is also a linear combination of the integers 17 and 41, so I can also reach a – b and b using the two moves, hence proving the inductive step. Therefore, the statement given in the beginning of this paragraph is true.

Now, we must consider what numbers actually appear in this sequence of tuples. Firstly, let’s find an invariant in this sequence of tuples. Note that the greatest common divisor of the pair of numbers in the tuple is the same for all tuples in the sequence. To see this, note that if d is a divisor of a and b, then it is also a divisor of a – b. Similarly, if d is a divisor of a – b and b, then it is also a divisor of a – b + b = a. So d is a common divisor for the first tuple if and only if it is a common divisor for the second tuple. So the set of common divisors for both of the tuples are identical, and since these sets are identical, the greatest elements of the sets are also identical, and the greatest elements of these sets are nothing but the greatest common divisors. So every tuple will have the same greatest common divisor of its two elements, so the first tuple will have the same greatest common divisor as the last tuple.

Note that the greatest common divisor of 17 and 41 (The first tuple) is 1. There can never be a negative number in these tuples, because the smaller number is always subtracted from the larger number, so the sequence only ends when one number becomes 0. Since 0 is divisible by all positive integers, and the greatest common divisor of the last tuple is 1, the second element of the last tuple must be 1. Since 1 appears in the last tuple, it is possible to reach the number 1 using these two moves. Hence it is possible to move 1 to the right, and since all positive integers can be reached through a series moves of length 1 to the right, all positive integers can be reached using the two moves, as desired.

To generalise this argument by replacing 17 and 41 with arbitrary positive integers a and b, it is not hard to see that the positive integers which can be reached using the two moves are those positive integers which are multiples of the greatest common divisor of a and b. This can easily be seen by replacing 17 and 41 with the arbitrary positive integers a and b in the argument above. In fact, this is a very well known fact in number theory which follows from Euclid’s Division Algorithm.

Don’t forget to check my blog next week for another fascinating problem!!

Problem: Consider a 6 by 6 grid where you start at the top left square of the grid. Is there a path from the top left corner of the grid to the bottom right square of the grid such that you visit each of the 35 squares except the starting square exactly once (You cannot revisit the starting square. Note that each move in a path is either one step in the vertical direction or one step in the horizontal direction. You can’t move diagonally)

Solution: The first step to solving this problem is to colour the squares of the 6 by 6 grid as in the picture shown below.

Now, notice a few things about this colouring. Firstly, a white square is only adjacent to black squares and a black square is only adjacent to white squares. So, with each move, the colour of the square I am on changes. Since there are 36 squares, exactly 35 moves have to be made in total, as the 35 squares apart from the starting square need to be visited exactly once.

Since the colour of the current square changes with every move, I will need to be on a square of a different colour after an odd number of moves. So, since I start on a white square and I make an odd number of moves, I must end on a black square. However, it is easy to see from the diagram above that the bottom right square is a white square. So, it is impossible to end on the bottom right square if I visit every square except the starting square exactly once. Hence, the answer to question posed at the beginning of this post is no!!

Don’t forget to check my blog next week for another fascinating problem!!

Image Source: http://www.murderousmaths.co.uk/books/MMoE/chess.htm

In the video posted below, I put light on the logic behind divisibility rules, and I also explain how can you create a divisibility rule for any positive integer.

The link of the video is:

https://www.youtube.com/watch?v=yFMiV-xiTY4&t=3s

The problem which I have solved below is Problem 4 from the 43rd International Mathematical Olympiad held in 2002

The problem which I have solved below is from the MIT Integration Bee, 2012. I found this problem a very interesting one pertaining to u-substitution.

The problem which I have solved below is from the 66th William Lowell Putnam Mathematical Competition held on Saturday, December 3, 2005. I found this problem very interesting as it harnessed my algebraic intuition.

The problem which I have solved below is from the 66th William Lowell Putnam Mathematical Competition held on Saturday, December 3, 2005